684. Redundant Connection

https://leetcode.com/problems/redundant-connection/description/?envType=daily-question&envId=2025-01-29

 

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

 

Example 1:

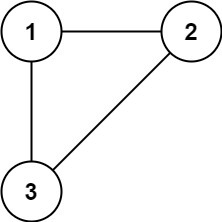
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

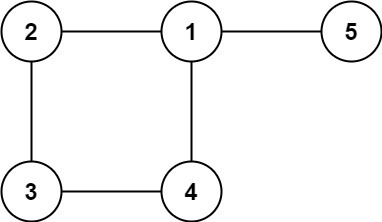
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

 

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

제거 가능한 간선 중 가장 마지막 간선을 반환하는 문제입니다.

이미 노드 A에서 B로 갈 수 있는 어떤 임의의 경로가 존재한다면, 새로 추가된 간선 A-B는 제거해도 무방합니다.
(이미 간접 경로가 존재하므로)

 

따라서, 두 노드의 연결 여부를 판단하는 쿼리를 O(NlogN)의 시간복잡도 내에서 구현해야합니다.
(총 N<=1000개의 쿼리가 주어지므로)

 

따라서, 우리는 이 문제를 Disjoint Set을 활용해 풀 수 있다는 것을 알 수 있습니다.
(두 트리의 병합 및 연결 여부 판단을 O(logN)에 처리 가능)

 

=============================================================

코드는 아래와 같으며,

전체 시간 복잡도는 N(전체 쿼리 수) x logN(쿼리 복잡도) = O(NlogN)입니다,

 

class Solution:

    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:

        parent = [i for i in range(len(edges)  + 1)]

        def find(a : int) -> int:

            if parent[a] == a:  return a

            parent[a] = find(parent[a])

            return parent[a]

        def union(a : int, b : int):

            parent[find(b)] = find(a)

        for a,b in edges:

            if find(a) == find(b): return [a,b]

            union(a,b)